Fibonacci Numbers Spelled Out
by Ivan Galkin,
U.MASS Lowell
Materials for 91.503 Algorithms
| "Spelled Out" series contains all derivations usually
omitted by gurus and left for the reader to agonize over. Spelled out documents
are written in a free style to ease the pain. |
1. Fibonacci Numbers, or "How many rabbits will you get after a year?"
Here they are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
each number is a sum of two previous.
We can write a difference equation for Fibonacci numbers as:
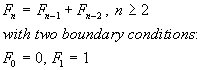
|
(1)
|
2. Generating Function Approach
A useful way to describe an integer sequence is to construct a generating
function B(x):
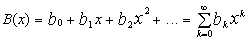
|
(2)
|
whose coefficients bi are the sequence. B(x)
is a power series over a purely formal variable x. ("Power" series
just indicates that the powers of x are used in the series.)
The whole point of building B(x) is to figure out an analytic
formula for those bi. The usual trick is to find a closed
form expression for B(x) and tweak it.
2.1 Closed-form expression
Some power series are able to converge to an expression which does not
include infinite summation anymore. For instance, an infinite sequence
of the numbers (dear to our hearts):
1, 2, 4, 8, 16, 32, 64, 128, 256 ...
can be represented by a generating function:

which can be, suprisingly, put in a closed form:
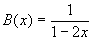
For this to happen, x must be less than 1 -- otherwise the sum terms grow
and it can not converge.
Just to give us a feeling, let's select x = 0.1:
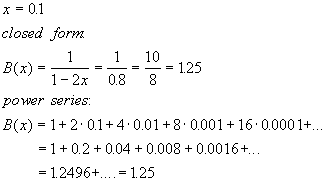
It works!
|
A popular closed form expression
|
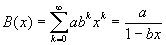
|
(3)
|
2.2 Closed-form Expression for Fibonacci Numbers' Generating Function
So the idea is to assume a generic generating function (2) with coefficients
representing the Fibonacci numbers. Now we have to find some regularity
in the behavior of the coefficients.
Here's the trick:
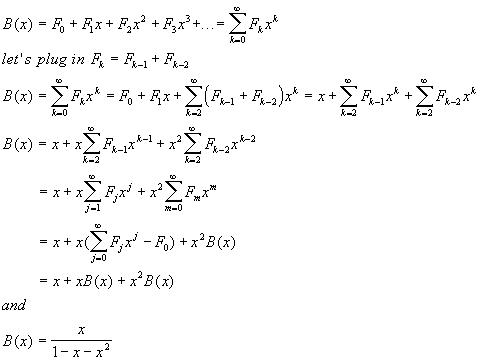
|
(4)
|
And this is a closed-form expression for the Fibonacci numbers' generating
function.
The point here is that generating function turns the recursive equation
(1) with two boundary conditions into something more managable.And it is
because it can kinda transform (n-1) terms into xB(x),
(n-2) into x2B(x), etc.
2.4. Verifying Closed-Form Expression for Fibonacci #s GF by Long Division
Well, I studied "stolbikom" division in USSR, so I apologize if my arrangement
on the paper look confusing to you. It sure does to me. Check here
for a polynomial division example I used to figure out US notation.
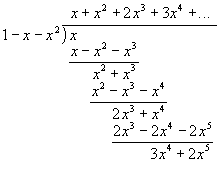
The point is -- here's our sequence 1, 1, 2, 3,
... er, where do I look for the answer, again? Oh well, the
top line. Now we see how GFs work -- if we expand them in series over xn,
the original sequence is generated.
2.5. Expanding Closed-form Expression for GF
The next step is to find a good (closed-form) expression for k-th
Fibonacci number. The basic idea is to expand the closed-form expression
for GF (4) back to the infinite power series. Well, there is a generic
way of expanding a ratio of polynomials into Taylor series around the poles.
Instead, we can use (courtesy of Bernulli) algebraic manipulation which
shall reduce (4) into a form of some known generating function expansion
(like (3)):
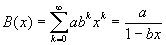
We shall find these a and b for the case of Fibonacci GF
(4).
1. First, we have to split quadratic polynomial in the denominator of
(4):
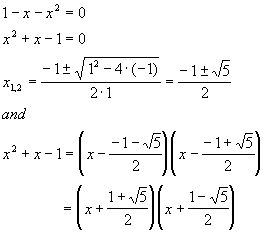
2. It really helps at this point to introduce a "Golden
Section" or "Divine Proportion", F:
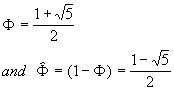
After that our generating function becomes:
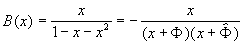
This is not good enough: we need constructions ( 1 - bx ) in the
denominator. So our next trick is:
3. 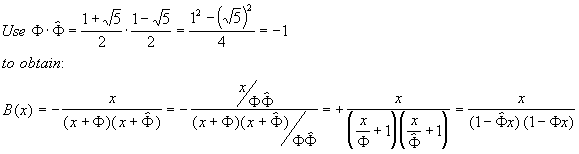
4. Now, we split the fraction
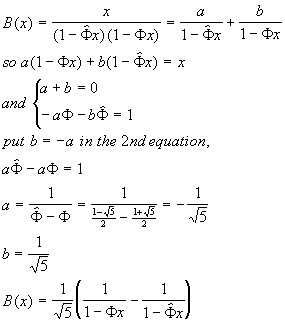
|
(6)
|
5. And, finally, we compare (6) to (3) to conclude:
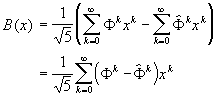
Here are our Fibonacci numbers:
|
Fibonacci Numbers, closed-form
|
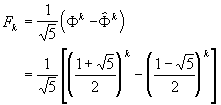 (7)
(7)
|
3. Characteristic Polynomial Approach
Another techcnique of solving difference equation (1) is to let Fn
to be a characteristic polynomial rn, which appears to
quickly reduce (1) to
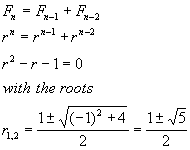
These roots are different from what we had in Section 2.The general solution
to equation Fn = rn will be all
possible combinations of roots r1 and r2:
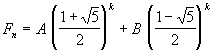
Constants A and B can be found from the boundary conditions
F0=0 and F1=1:
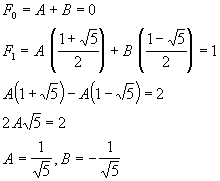
So we arrive at familiar expression for Fibonacci numbers (7).
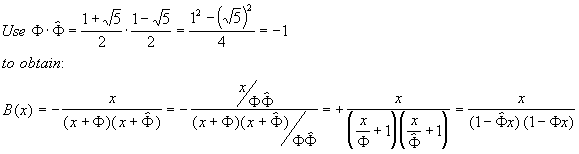
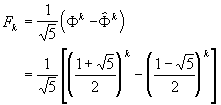 (7)
(7)