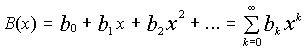
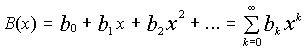 |
(1)
|
So the idea is to assume a generic generating function (1) with coefficients representing the number of binary trees. Now we have to find some regularity in the behavior of coefficients.
We can start with analyzing trees with small n. Apparently,
b1 is 1, and b2 is 2. The b0
coefficient is somewhat artificial, its the no-nodes tree
which is, I guess, the only one. Further analysis gives the following idea:
if a binary tree has n nodes, then there must be one node as the
root and two subtrees. The total number of nodes in the subtrees must be
n-1, and either of them may be empty. Assuming k nodes
in the left subtree, the right subtree then has n-k-1 nodes, k
going from 0 to n-1. The root node is always there, and therefore
the tree configurations differ only by the configuration of subtrees. The
total number of possible trees on n nodes can then be expressed
as:
|
|
(2)
|
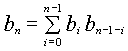 |
(3)
|
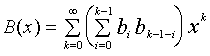 |
(4)
|
Regretfully, we just claimed that the expression in the brackets is invalid for k = 0. I donít know how to deal with this inconsistency.
The next step is to convert the sum-of-product expression in (4)
to an appropriate product-of-sum expression. This operation actually represents
the rule of multiplication of polynomials [Henrici, 1982, p 382]:
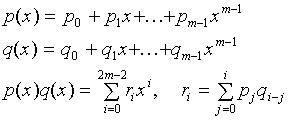 |
(5)
|
In our case p(x) and q(x) are the same B(x).
We can now apply the rule (5) in the backward direction to (4) or, better
yet, obtain an expression for B(x)2 and compare it to
(4):
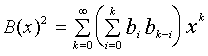 |
(6)
|
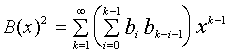 |
(7)
|
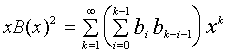 |
(8)
|
we need one term with k=0 for the right part to become (4).
Adding 1 to both sides,
|
|
(9)
|
Two solutions for B(x) in (9) are
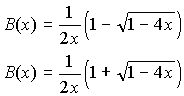 |
(10)
|
The second root turns to infinity when x is 0 so that B(0) does not exist. Therefore we use the first root for further manipulations.
The Binomial Theorem can now be applied to the square root in (10)
to reduce it to the form with xk and the coefficients
that we are looking for. The Binomial theorem can be written as
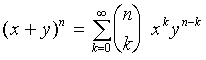 |
(11)
|
then
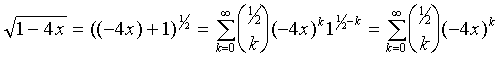 |
(12)
|
Substituting (12) into our valid solution (10), we have
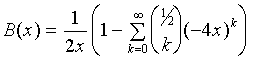 |
(13)
|
Letís use the term with k=0 to cancel 1 inside the brackets:
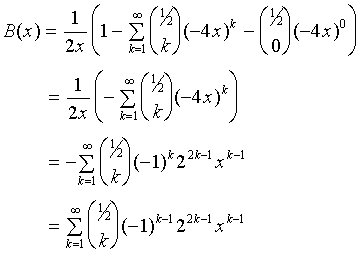 |
(14)
|
Changing index k to index n running from 0 to ¥
where k runs from 1 to ¥ , we have
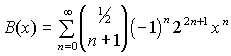 |
(15)
|
and, therefore,
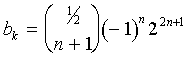 |
(16)
|
The final simplifications of the binomial coefficient are identical
to the Example 1b.
REFERENCES
Henrici, P. Essentials of Numerical Analysis with Pocket Calculator Demonstrations. John Wiley & Sons, NY., 1982.