Crash Introduction to Artificial Neural Networks

1. Neurobiological Background

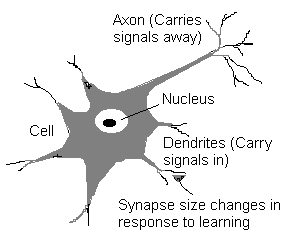
The Structure of Neuron

Source of the diagram: NIBS Pte Ltd.

This is a result worth of the Nobel Prize [1906]. The neuron is a many-inputs / one-output unit. The output can be excited or not excited , just two possible choices (like a flip-flop). The signals from other neurons are summed together and compared against a threshold to determine if the neuron shall excite ("fire"). The input signals are subject to attenuation in the synapses which are junction parts of the neuron.

The next important step was to find that the synapse resistance to the incoming signal can be changed during a "learning" process [1949]:
 

This discovery became a basis for the concept of associative memory (see below).

2. Artificial Neuron

The Artificial Neuron is actually quite simple. All signals can be 1 or -1 (the "binary" case, often called classic spin for its similarity with the problem of disordered magnetic systems). The neuron calculates a weighted sum of inputs and compares it to a threshold. If the sum is higher than the threshold, the output is set to 1, otherwise to -1.

3. Artificial Neural Networks (ANN)

The power of neuron comes from its collective behavior in a network where all neurons are interconnected. The network starts evolving: neurons continuously evaluate their output by looking at their inputs, calculating the weighted sum and comparing to a threshold to decide if they should fire. This is highly complex parallel process whose features can not be reduced to phenomena taking place with individual neurons.

One observation is that the evolving of ANN causes it to eventually reach a state where all neurons continue working but no further changes in their state happen. A network may have more than one stable states, and it is obviously determined (somehow) by the choice of synaptic weights and thresholds for the neurons.

3.1. Perceptron

3.1.1. Feed-forward Configuration

Another step in understanding of ANN dynamics was made with introduction and analysis of a perceptron [Rosenblat, 1958], a simple neural network consisting of input layer, output layer, and possibly one or more intermediate layers of neurons.
 

Once the input layer neurons are clamped to their values, the evolving starts: layer by layer, the neurons determine their output. This ANN configuration is often called feed-forward because of this feature. The dependence of output values on input values is quite complex and includes all synaptic weights and thresholds. Usually this dependence does not have a meaningful analytic expression. However, this is not necessary: there are learning algorithms that, given the inputs, adjust the weights to produce the required output.

So, simply put, we created a thing which learns how to recognize certain input patterns.

There is a training phase when known patterns are presented to the network and its weights are adjusted to produce required outputs. Then, there is a recognition phase when the weights are fixed, the patterns are again presented to the network and it recalls the outputs.

3.1.2. Classification/Prediction ANN

Among many applications of the feed-forward ANNs, the classification or prediction scenario is perhaps the most interesting for data mining. In this mode, the network is trained to classify certain patterns into certain groups, and then is used to classify novel patterns which were never presented to the net before. (The correct term for this scenario is schemata-completion ).
 

3.1.3. Application of ANN to Memory Designs

• Content-Addressable and Associative Memory: the information is stored, retrieved, and modified based on the data itself, not its arbitrary storage location.
• Error-Correction and Partial-Contents Memory: the memory capable of retrieving the stored information being presented with a noisy or incomplete original sample.

3.1.4. Training Algorithms for Feed-forward ANNs

The most popular algorithm for adjusting weights during the training phase is called back-propagation of error. The initial configuration of ANN is arbitrary; the result of presenting a pattern to the ANN is likely to produce incorrect output. The errors for all input patterns are propagated backwards, from the output layer towards the input layer. The corrections to the weights are selected  to minimize the residual error between actual and desired outputs. The algorithm can be viewed as a generalized least squares technique applied to multilayer perceptron. The usual approach of minimizing the errors leads to a system of linear equations; it is important to realize here that its solution is not unique. The time spent on calculating weights is much longer than the time required to run the finalized neural network in the recognition mode, so the resulting weights are arguably eligible for copyright protection.

3.2. Energy Function Analysis

3.2.1. Energy Function

Introduction of an energy function concept, due to Hopfield [1982-1986], led to an explosion of work on neural networks. The energy function brought an elegant answer to a tough problem of ANN convergence to a stable state:
 

 
The specifics of ANN evolving allowed to introduce this function which always decreases (or remains unchanged) with each iteration step. Evolving of ANNs and even their specifications started to be described in terms of the energy function.

3.2.2. Global and Local Minima of Energy Function

Apparently, letting an ANN to evolve eventually shall lead it to a stable state where the energy function has a minimum and can not change further. The information stored in the synaptic weights W_ij therefore corresponds to some minima of the energy function where the neural network ends up after its evolving.
 

When the input neurons are clamped to the initial values, the network obtains certain energy as indicated by a ball in the above figure. Further evolving will cause the ball to slide to the nearest local minimum.

3.2.3. Training of ANN in Terms of Energy Function

Training of a network is adjustment of weights to match the actual outputs to desired outputs of the network. The expression for the energy function contain the weights, and we can think of the training process as "shaping" of the energy function.

3.3. Mean-Field Theory

The Mean Field Theory (MFT) [Hopfield, 1982] treats neurons as objects with continuous inputs and output states, not just +1 or -1, as in the "classic spin" approach. In the network of neurons, MFT introduces statistical notion of "thermal average", "mean" field V of all input signals of a neuron. To provide the continuity of the neuron outputs, a notion of sigmoid function, g(u), is introduced to be used instead of a simple step-function threshold.

	Classic Spin	Mean Field
Neuron State	Si = -1 or +1
Energy
Neuron Input Field
Evolving	Si = sign( Ui )

The most popular sigmoid function for ANNs is tanh:

Sigmoid Function

Sigmoid function makes processing in neurons nonlinear:

3.4. Feed-back ANN

This configuration of neural networks does not assume propagation of input signal through the hidden layers to the output layers; rather, the output signals of neurons are fed again to the inputs so that evolving continues until stopped externally

The feed-back ANNs best suited for optimization problems where the neural network looks for the best arrangement of interconnected factors. The arrangement corresponds to the global minimum of the energy function (see section 3.2.2). Feed-back ANNs are also used for error-correction and partial-contents memories (see section 3.1.3) where the stored patterns correspond to the local minima of the energy function.

3.5. Search For the Global Minimum

Optimization problems require a search for the global minimum of the energy function. If we simply let ANN evolve it will reach the nearest local minimum and stop there. To help with the search, one way is to allow for energy fluctuations in ANN by introducing a "probability" that the neuron should fire when the local field is high or should stay calm if the local field is low. In other words, certain amount of chaos is introduced into the ANN evolving process, which can be also imagined as "shaking" of the system where the ball slides along the energy function curve.

3.5.1. Simulated Annealing Schemes

If we allow "shaking" of the evolving process, it is important not to shake the system out of the global minimum. In other words, shaking should be made lighter as the network evolves. Due to similarity of annealing technique used in metal industry, the temperature scenarios are collectively called simulated annealing.  There are a few popular stochastic simulated annealing schemes (Heat Bath, Metropolis, Langevin).

Training of the neural networks is an optimization problem itself. Simulated annealing schemes are applied there, too (see Section 4.2).

3.5.2. MFT Tunneling

Treatment of ANN evolving within the MFT approach allows for tunneling of the energy into the neighboring (lower) maximum of the energy function.

4. Advanced Topics

4.1. Underfitting and Overfitting of ANN

4.1.1. Fitting the Data

Application of neural networks to Data Mining uses the ability of ANN to build models of data by capturing the most important features during training period. What is called "statistical inference" in statistics, here is called "data fitting". The critical issue in developing a neural network is this generalization: how well will the network make classification of patterns that are not in the training set? Neural networks, like other flexible nonlinear estimation methods such as kernel regression and smoothing splines, can suffer from either underfitting or overfitting.

4.1.2. Dealing with Noisy Data

The training set of data might as well be quite "noisy" or "imprecise". The training process usually relies on some version of least squares technique which ideally should abstract from the noise in the data. However, this feature of ANN is dependent on how optimal is the configuration of the net in terms of number of layers, neurons and, ultimately, weights.

A network that is not sufficiently complex can fail to detect fully the signal in a complicated data set, leading to underfitting. A network that is too complex may fit the noise, not just the signal, leading to overfitting. Overfitting is especially dangerous because it can easily lead to predictions that are far beyond the range of the training data with many of the common types of neural networks. But underfitting can also produce wild predictions in multilayer perceptrons, even with noise-free data.

4.1.3. Avoiding Underfitting and Overfitting

The best way to avoid overfitting is to use lots of training data. If you have at least 30 times as many training cases as there are weights in the network, you are unlikely to suffer from overfitting. But you can't arbitrarily reduce the number of weights for fear of underfitting.

Given a fixed amount of training data, there are at least five effective approaches to avoiding underfitting and overfitting, and hence getting good generalization:

• Model selection
• Jittering
• Weight decay
• Early stopping
• Bayesian estimation

4.2. Training ANN as an Optimization Task

Training a neural network is, in most cases, an exercise in numerical optimization of a usually nonlinear function. Methods of nonlinear optimization have been studied for hundreds of years, and there is a huge literature on the subject in fields such as numerical analysis, operations research, and statistical computing, e.g., Bertsekas 1995, Gill, Murray, and Wright 1981. There is no single best method for nonlinear optimization. You need to choose a method based on the characteristics of the problem to be solved. For functions with continuous second derivatives (which would include feedforward nets with the most popular differentiable activation functions and error functions), three general types of algorithms have been found to be effective for most practical purposes: For a small number of weights, stabilized Newton and Gauss-Newton algorithms, including various Levenberg-Marquardt and trust-region algorithms are efficient. For a moderate number of weights, various quasi-Newton algorithms are efficient. For a large number of weights, various conjugate-gradient algorithms are efficient. All of the above methods find local optima. For global optimization, there are a variety of approaches. You can simply run any of the local optimization methods from numerous random starting points. Or you can try more complicated methods designed for global optimization such as simulated annealing or genetic algorithms (see Reeves 1993 and "What about Genetic Algorithms and Evolutionary Computation?").