Enumeration of the Binary Trees (Catalan numbers).

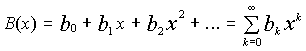
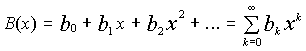(1)

So the idea is to assume a generic generating function (1) with coefficients representing the number of binary trees. Now we have to find some regularity in the behavior of coefficients.

We can start with analyzing trees with small n. Apparently, b₁ is 1, and b₂ is 2. The b₀ coefficient is somewhat artificial, its the no-nodes tree which is, I guess, the only one. Further analysis gives the following idea: if a binary tree has n nodes, then there must be one node as the root and two subtrees. The total number of nodes in the subtrees must be n-1, and either of them may be empty. Assuming k nodes in the left subtree, the right subtree then has n-k-1 nodes, k going from 0 to n-1. The root node is always there, and therefore the tree configurations differ only by the configuration of subtrees. The total number of possible trees on n nodes can then be expressed as:
 

(2)

This formula expresses the specifics of our problem. The number of terms in (2) varies depending on n. The expression is invalid for n=0; for n=1 we have just one term b₀b₀; for n=2 there are two terms b₀b₁ + b₁b₀. Thus, we can rewrite (2) more accurately as
 

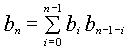(3)

Substituting (3) into (1), we get
 

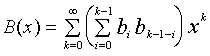(4)

 

Regretfully, we just claimed that the expression in the brackets is invalid for k = 0. I don’t know how to deal with this inconsistency.

The next step is to convert the sum-of-product expression in (4) to an appropriate product-of-sum expression. This operation actually represents the rule of multiplication of polynomials [Henrici, 1982, p 382]:
 

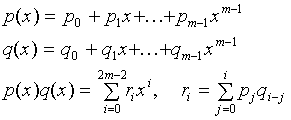(5)

which should be used in the reverse direction for our purposes.
 
Multiplication of polynomials (5) may be actually shown to be identical to the operation of convolution if we let n = 2m and pad coefficients p_i and q_i in (5) with m zeroes so that upper summation limit for r_i may be extended to n-1. I had difficulty to use the Convolution Theorem as instructed in the homework problem description, as its description in [Henrici, 1982, p.385] contains the Hadagard product of two Fourier transforms and the conjugate Fourier transform used to speed up the conventional convolution.

In our case p(x) and q(x) are the same B(x). We can now apply the rule (5) in the backward direction to (4) or, better yet, obtain an expression for B(x)² and compare it to (4):
 

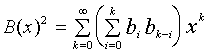(6)

 
Comparing (6) to (4), we see that, for the sake of finding the similarity, summation index should be changed from k to k-1:
 

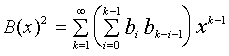(7)

After multiplying both parts by x:
 

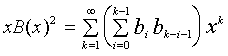(8)

we need one term with k=0 for the right part to become (4). Adding 1 to both sides,
 

(9)

Two solutions for B(x) in (9) are
 

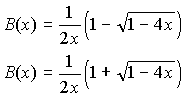(10)

The second root turns to infinity when x is 0 so that B(0) does not exist. Therefore we use the first root for further manipulations.

The Binomial Theorem can now be applied to the square root in (10) to reduce it to the form with x^k and the coefficients that we are looking for. The Binomial theorem can be written as
 

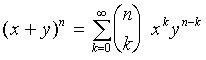(11)

then
 

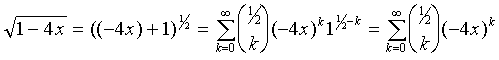(12)

Substituting (12) into our valid solution (10), we have
 

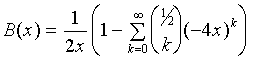(13)

Let’s use the term with k=0 to cancel 1 inside the brackets:
 

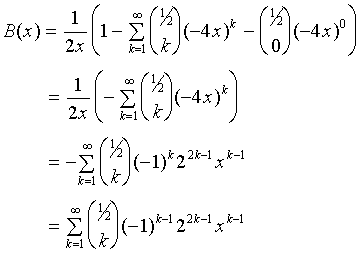(14)

Here we used the fact thatis 1. I failed to figure out why this is true.

Changing index k to index n running from 0 to ¥ where k runs from 1 to ¥ , we have
 

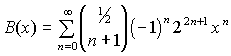(15)

and, therefore,
 
 

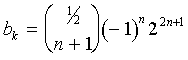(16)

The final simplifications of the binomial coefficient are identical to the Example 1b.
 

REFERENCES

Henrici, P. Essentials of Numerical Analysis with Pocket Calculator Demonstrations. John Wiley & Sons, NY., 1982.