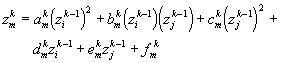
| Year | Product | Price | Availability |
| 1994 | AIM for DOS 1.1 | $200 | discontinued |
| 1994 | AIM for Windows 2.0 | $1,000 | discontinued |
| 1995 | ModelQuest (TM) / ModelQuest Prospector | $1,000 | discontinued |
| 1996, Oct. | ModelQuest Expert | $4,000 | discontinued |
| 1997, Apr. | ModelQuest Expert 2.0 w/StatNet Expert | $6,000 | |
| 1997, June | ModelQuest Miner | discontinued | |
| 1997 Oct. | ModelQuest Enterprise | $60,000 | |
| 1997 Nov. | ModelQuest MarketMiner | $60,000 |
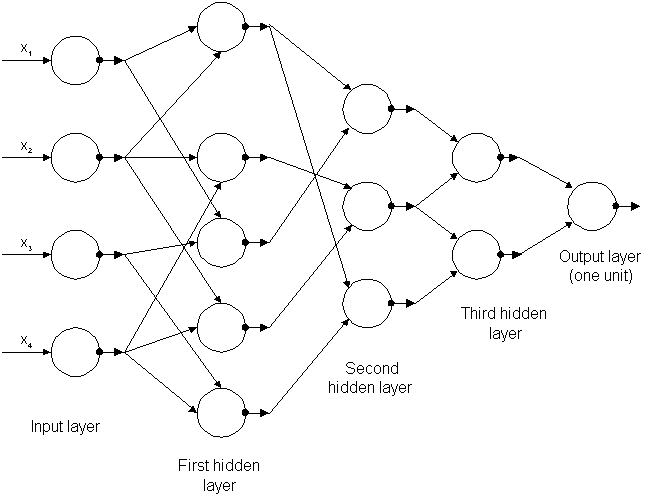
Ivakhnenko made the neuron a more complex unit featuring a polynomial transfer function. The interconnections between layers of neurons were simplified, and an automatic algorithm for structure design and weight adjustment was developed.
 |
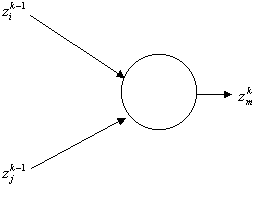
Output of GMDH neuron
|
|
|
 |
The basic idea of GMDH adjustment is that each neuron wants to produce y at its output (i.e., the overall desired output of the network). In other words, each neuron of the polynomial network fits its output to the desired value y for each input vector x from the training set. The manner in which this approximation is accomplished is through the use of linear regression.
The training set is used to guide the process of adjusting the six weights of each neuron in the layer under construction. Each example in the training set gives one linear equation on six unknowns. Then the mean square technique is used to derive the best combination of six weights (for each neuron! plenty of matrix algebra...).
Usually, the mean square error of y' differs enormously from one neuron to another. The next step in adjusting the layer is eliminating the neurons of the layer which have an unacceptably large error. The definition of "unacceptably large" is left to the user. Certain heuristics exist to help automatic selection of the thershold. The elimination of "bad" neurons effectively reduces otherwise overwhelming combinatorial explosion of building all possible C(Mk-1, 2) configurations.
The process of building the network continues layer by layer until a stopping criterion is satisfied. Usually, the mean square error of the best performing neuron is lower with each subsequent layer until an absolute minimum is reached. If further layers are added, the error of best performaing neuron actually rises. After the last layer is determined, each of the preceding layers undergoes anouther round of trimming to exclude those neurons that do not contribute into the final output.
The following is comparison results from here.
| Neural networks | Statistical learning GMDH networks | |
| Data analysis | universal approximator | universal structure identificator |
| Analytical model | indirect approximation | direct approximation |
| Architecture | preselected unbounded network structure; experimental selection of adequate architecture demands time and experience | bounded network structure evolved during estimation process |
| Network synthesis | globally optimized fixed network structure | adaptively synthesized structure |
| Apriori Information | without transformation in the concepts of neural networks not usable | can be used directly to select the reference functions and criteria |
| Self-organization | deductive, subjective choice of layers number and number of nodes | inductive, number of layers and of nodes estimated by minimum of external criterion (objective choice) |
| Parameter estimation | in a recursive way;
demands long samples |
estimation on training set by means of maximum likelihood techniques, selection on testing set (may be extremely short or noised) |
| Optimization | global search in a highly multimodal space, result depends from initial solution, tedious and requiring from user to set various algorithmic parameters by trial and error, time-consuming technique | simultaneously optimize the structure and dependencies in model, not time-consuming technique, inappropriate parameters not included automatically |
| Access to result | available transiently in a real-time environment | usually stored and repeatedly accessible |
| Initial knowledge | needs knowledge about the theory of neural networks | necessary knowledge about the kind of task (criterion) and class of system (linear,non-linear) |
| Convergence | global convergence is difficult to guarantee | model of optimal complexity is founded |
| Computing | suitable for implementation using hardware with parallel computation | efficient for ordinary computers and also for massively parallel computation |
| Features | general-purpose, flexible, non-linear (especially linear) static or dynamic models | general-purpose, flexible linear or nonlinear, static or dynamic, parametric and non-parametric models |